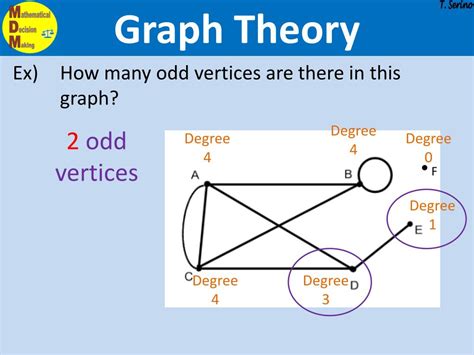
vertices of odd degree|Proving that the number of vertices of odd degree in any graph G is even : Cebu In this video graph theory lesson, we'll prove that every graph has an even number of odd degree vertices, to understand just why it's true! For this proof, we'll . Wyoming Brewers Festival Brew Battle 2024. Thanks to all who participated in the Wyoming Brewers Festival Brew Battle 2024. There were 15 entries judged and 75 registered participants, judges, and stewards. Best of Show Winners . Best of Show – Beer. Place Brewer Entry Name Style Club; 1st:
vertices of odd degree,Euler’s Theorem \(\PageIndex{1}\): If a graph has any vertices of odd degree, then it cannot have an Euler circuit. If a graph is connected and every vertex has an even degree, then it has at least .To prove that the number of odd vertices in a simple graph is always even, we can use the Handshaking Lemma, which states that the sum of the degrees of all vertices in a graph .
In this video graph theory lesson, we'll prove that every graph has an even number of odd degree vertices, to understand just why it's true! For this proof, we'll . An undirected graph has an Eulerian path if and only if it is connected and has either zero or two vertices with an odd degree. If no vertex has an odd degree, .The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant, so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degre.
A graph has an Euler path if and only if there are at most two vertices with odd degree. Since the bridges of Königsberg graph has all four vertices with odd degree, there is no . Odd Vertex. A graph vertex in a graph is said to be an odd node if its vertex degree is odd .

The algorithm produces Eulerian circuits, but it can be modified to produce Eulerian paths if there are two vertices of odd degree. Suppose every vertex has even degree. Start with a vertex \( v \) and follow a path . In every graph, the number of vertices of odd degree is even. Proof Idea. Otherwise, the sum of the degrees of all vertices would be odd, which contradicts the theorem above. Example \(\PageIndex{3}\) An odd fellow throws an odd party and invites an even number of other equally-odd people. Each odd person at the party is friends .vertices of odd degreeJust as Euler determined that only graphs with vertices of even degree have Euler circuits, he also realized that the only vertices of odd degree in a graph with an Euler trail are the starting and ending vertices. For .In this situation the odd degree are 1 or 3 in two vertices.In the undirected graph degree one have exactly connection between two vertex. In the case of 3 vertices both vertex have a loop (the loop consider as degree two in undirected graph) and a connected path between them. There fore exactly two vertices of odd degree then there is a path . The sum of the degrees of vertices in a graph is exactly twice the number of edges, and thus even. The sum of the degrees of 'even' vertices is clearly even. Which means that the sum of the degrees of 'odd' vertices must be even as well (else the sum of both would be odd). Since only an even number of odd integers sum up to an even . An undirected graph has an even number of vertices of odd degree. Proof : Let and be the sets of vertices of even and odd degrees respectively. We know by the handshaking theorem that, So, The sum of degrees of vertices with even degrees is even. The LHS is also even, which means that the sum of degrees of vertices with odd .

THEOREM 2.3. A connected graph with 2k odd vertices contains a family of k distinct trails which, together, traverse all edges of the graph exactly once. PROOF. Let the odd vertices in the graph be denoted by in some order. a1,a2, .,ak . $\begingroup$ If I add connect ab and cd there's going to be 0 odd degree vertex so there is at least one euler circuit in the new graph, and then if I get rid of the two edge the circuit is now disconnect but there will be two separate kinda "trail" thing.Proving that the number of vertices of odd degree in any graph G is evenThe graph could not have any odd degree vertex as an Euler path would have to start there or end there, but not both. Thus for a graph to have an Euler circuit, all vertices must have even degree. The converse is also true: if all the vertices of a graph have even degree, then the graph has an Euler circuit, and if there are exactly two .
vertices of odd degree|Proving that the number of vertices of odd degree in any graph G is even
PH0 · Proving that the number of vertices of odd degree in any graph G is even
PH1 · Proving that the number of vertices of odd degree in any
PH2 · Proof: Every Graph has an Even Number of Odd Degree Vertices
PH3 · Odd Vertex
PH4 · Eulerian Path
PH5 · Degree (graph theory)
PH6 · 9.4: Traversals
PH7 · 6.3: Euler Circuits
PH8 · 4.4: Euler Paths and Circuits
PH9 · 12.6 Euler Trails